Local Collision Avoidance

See ORCA in action at github.com/downflux/go-orca.

Consider a rectangle. If we were to double the length and width of the box, we quadruple the total area – the area of a 2D object increases much faster than its characteristic length. We sometimes refer to this phenomena, and others like it, as the curse of dimensionality. The basic idea is that when there are decisions to be made, adding more factors to consider is really slow.

We are using this rectangle to represent the world map in DownFlux. One of the fundamental things we need to do in a real-time strategy game is to order units to move around the map. Pathfinding techniques such as A* are great with finding the optimal global path – but for large maps, we have to search a lot due to the curse. This problem balloons when we consider the amount of units that can typically generate in a RTS, e.g. on the order of thousands. Furthermore, remember that all of these units have hitboxes – when we run pathfinding, not only do we need to ensure units do not collide with walls, we also need to make sure units don’t collide with one another. As the units are all moving, the only way we can do this within the A* framework is to recalculate the paths. A lot.

Putting all of this together, we expect that pathfinding will be a significant drain on our computing resources, of which we have very little when taking into consideration these computations will all need to be completed within the fraction of a second comprising a server tick.

In order to reduce the pathfinding computation time then, it appears we need to tackle the problem in two fronts –

1. find a way to apply the results of a single A* calculation to multiple units, and

2. reduce the number of A* pathfinding calculations which need to occur due to potential collisions

A common command pattern in real-time strategy games is for a player to issue a move command to an entire group of units. A natural inclination then, is to run A* only on the single move target for all the units currently selected. But doing so will naturally generate numerous collision events as the units converge on a common target – so we need a way to calculate local unit movement without falling back to A*. We need local collision avoidance detection.

ORCA

Optimal Reciprocal Collision Avoidance (ORCA) is a technique which guarantees local collision avoidance for a set of independent agents; that is, we can simulate a bunch of moving objects, and ensure that the objects do not overlap, without (or with very limited) knowledge of any global state. This is incredibly applicable to our problem because we can bypass all collision detection A* invocations, which in theory will drastically reduce the computational load

ORCA achieves collision avoidance in two steps –

1. calculating all agent-agent interactions and coming up with a characteristic velocity which avoids collisions

    f(a, b) -> v
   

2. given all such velocities, calculate a velocity for each agent that accounts for all potential upcoming collisions i.e., a fold operation

    g({v<sub>a</sub>}) -> v
   

When we apply these steps to all agents, we will get an agent {a: v} map, where there is a guarantee no collisions will occur if the agent sets their velocity to the prescribed output. What remains is to describe how these two steps actually work. We will focus on the characteristic collision avoidance velocity here, and leave the second step to a future post.

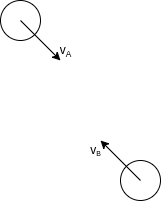
Consider two agents that are currently moving towards each other.

Figure 1: Two agents in position (p-)space heading towards one another.

In order to determine if these two objects will collide, we can systematically construct a velocity obstacle (VO) object in velocity (v-)space (Figure 2). The VO object is defined by two fundamental properties –

1. the shape of the central blockage¹ of the VO object, and

2. the coordinates of the center-of-mass of this blockage is away from the origin of v-space, which can be calculated from the relative velocities of the two objects.

The shape of the central blockage is defined to be the set of all relative² velocities between two objects which will result in collision, and the VO “cone” is built from extending a line from the origin to the edge of the blockage.

Any relative velocity between the two objects that fall within this cone indicates that the two objects will collide at some point in the future, assuming the velocities stay constant.

Figure 2: Velocity object between the two agents. The left figure demonstrates the intuitive construction of a velocity cone between two objects – here, we find the velocities of the bottom agent that will result in the two agents colliding. The right figure demonstrates a rough construction of the velocity obstacle object created by the agents in Figure 1. Note that the circle here defines the characteristic “width” of the cone, and whose radius is proportional to r_A + r_B.

We note that the distance from the v-space origin to the collision artifact (i.e. disc) is a function of time – that is, we will only achieve a collision if the velocity remains unchanged while the distance between the two agents shrinks. If our simulation time is very short (smaller than the time it would take to achieve collision) we should be able to proceed with the given velocity, even if it will eventually cause a collision. Thus, we can consider a truncated VO object, where the base of the circle has radius r₀ / 𝜏, and 𝜏 is the simulation timestep. For example, if we set

𝜏 = 1

in Figure 2, the base of the truncated VO object is just the solid circle, and the VO object points away from the origin. To reiterate, relative velocities between the two agents which fall inside this truncated cone will cause a collision within the next timestep.

Given a VO cone, it becomes fairly simple to generate a velocity which will avoid collision – this is the projected normal vector u onto the edge of VO. Because the algorithm is reciprocal, we can assume³ the opposing agent will also move to avoid the collision – thus, we only need to alter the velocity of each agent by ||u||/2 (directed away from one another in p-space). Note any relative velocity outside the VO object will ensure the two agents will not collide – because of reasons⁴, we narrow this search space to a half-plane⁵ ORCA_A|B for agent A, which is orthogonal to u and passes through the minimally-adjusted velocity v_A + u/2 (see Figure 3).

Figure 3: Construction of the ORCA half-plane of agent A given agent B. Note that u points to the closest point on the VO object from the relative velocity, and thus by definition is perpendicular to the surface of VO. Here, F(ORCA_A|B) indicates the direction of the half-plane – that is, the region in v-space which are permissible velocities for agent A.

We will leave discussion of how to use these ORCA planes to the next part.

Works Cited

• van den Berg et al. “Reciprocal n-Body Collision Avoidance.” 2011.

• Snape et al. “Reciprocal Collision Avoidance and Navigation for Video Games.” 2012.

• Sunshine-Hill, Ben. “RVO and ORCA: How They Really Work.” 2017.

• Snape, James. snape/RVO2. 2021.⁶

Notes